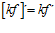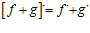Formulas de Integracion

Secciones Cónicas

Son aquéllas secciones que resultan al intersecar una superficie cónica de revolución con un plano. Según la posición del plano secante, en la superficie pueden obtenerse una circunferencia, parábola, elipse hipérbola. Cumpliéndose que el conjunto de puntos que forma cada cónica tienen una misma propiedad lo cual es característica fundamental de lo que en geometría llamamos lugar geométrico. 

Comenzaremos a revisar las aplicaciones:

CIRCUNFERENCIA 

Se la puede denominar como una linea curva cerrada que consta de una sucesión de puntos llamados centro. la cual forma un circulo

Formula general de la circunferencia:

Con centro en el origen (0,0) y radio “r”

Con centro en el punto (h,k), y radio “r”

Aplicaciones de la circunferencia en la Arquitectura:

La circunferencia ha sido considerada desde la antigüedad como símbolo de perfección, debido a su simetría. Partiendo de esto se puede notar que la circunferencia permite muchas facilidades a un arquitecto ya que tiene muchas ventajas el trabajar con la misma, por ejemplo:

- Ahorro en superficie de muros y cerramientos.

- Aumento de la eficiencia energética, gracias a una menor superficie de                transferencia de calor.

- Un mejor comportamiento frente a los vientos y la  radiación solar.  

Aunque hay que decir, que no se da mucho la utilización de la circunferencia en edificios, ya que presenta varias dificultades, como el tiempo, se tardaría mucho realizar una construcción circular, además sería complicada la realización de inmuebles que se acoplen a la construcción. Y es por eso que se lo utiliza más en cúpulas, estadios, piletas de parques, etc.

Piletas

Farmacia placebo -  Atenas

Estadio Maracana - Brasil

Farmacia placebo -  Atenas

El Templo del Cielo en Beijing

                                                               

 


 

  EJEMPLO

El edificio cuenta con un total de 23 pisos y un área construída de  48,000 metros cuadrados.

Edificio Fangyuan Mansion de Shenyang - China

1. Dados los puntos (-3 , 5) y (7 , -3). Hallar el radio, ecuación y gráfica.

Centro                                                            Radio                                             Ecuacion

c= (-3+7)/2 , (5-3)/2                               r2 = √(x2-x1)2 + (y2-y1)2           (X – h)2 + (Y – K)2 = r2

c= (2,1)                                                   r2 = √(7-2)2 + (3+1)2                  (X – 2)2 + (Y – 1)2 = 6.52

                                                                r = 6,4                                          (X – 2)2 + (Y – 1)2 = 42.2

 ELIPSE  
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría, con ángulo mayor que el de la generatriz respecto del eje de revolución. Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.  

Formula general de la elipse:

          

                                
 Aplicaciones de la elipse en la Arquitectura:

La elipsis se la utiliza en la arquitectura especialmente en anfiteatros, que se los construía en la antigüedad, también hay estadios elípticos, tal el caso de nuestro estadio el de Loja que se llama “Reina del Cisne” tiene una forma elíptica, en Iglesias, entre otras más.

Estadio “Reina del Cisne”

                                      Plaza San Pedro- Roma

                                           EJEMPLO

                 

Un ejemplo es la iglesia del Monasterio de San Bernardo, más conocido por "Las Bernardas" en Alcalá de Henares. Un templo con una única nave y planta elíptica, con cúpula del mismo trazado. En sus muros se abren seis capillas, cuatro de ellas también de planta elíptica, con diferentes tamaños de sus portadas.

1. Hallar la ecuación de la elipse cuyos focos son los puntos $(-4,3)$ y $(4,3)$, con vértices $(-8,3)$,$(8,3)$. Haga un bosquejo de la gráfica. 

Solución:
Calculemos la medida del eje mayor y el centro de la elipse:

Eje mayor	$$=	Distancia de $V$ a $V\text{'}$
$$2a	$$=	$\sqrt{(-8-8}$ )2 +(3-3 )2
$$2a	$$=	$$16
$$a	$$=	$$8

Note que Centro $=(h,k)$ donde $k=3$ cálculemos el valor de $h$
Si $V\text{'}=(h+a,k)$ y temenos que $V\text{'}=(8,3)$:

$$                                                       h+a	$$=	$$8
$$                                                       h+8	$$=	$$8
$$                                                   h	$$=	$$0

Por lo tanto el centro de la elipse es el punto $(0,3)$. Además si $F\text{'}=(h+c,k)$ y $F\text{'}=(4,3)$ como $h$ es cero tenemos que $c=4$

Cálculemos $b$.

$$                                                       b	$$=	$\sqrt{a^2}$ - c2
$$                                                       b	$$=	$\sqrt{8^2}$ - 42
$$                                                       b	$$=	$$48
$$                                                       b	$$≈	$$6.9

Finalmente sustituyendo en la ecuación de la elipse trasladada temenos:

$\frac{x^2}{}$ 64 + (y-3 )2 48 =1  

                                                                            PARÁBOLA

En matemáticas, una parábola es la sección cónica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta. Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamada directriz.

Formula general de la parábola:

y2+Dx+Ey+F=0

x2+Dx+Ey+F=0

Aplicaciones de la Parábola en la Arquitectura:
Se la utiliza mucho en puentes, ya que tiene buena resistencia estructura, también se la utiliza en puertas, el caso de la Catedral de Loja, sus puertas tienen forma de parábola, así también conchas acústicas, el caso de la cafetería, de la UTPL, tiene el techo parabólico.

Puente de Zamora   

                                  

                                   

                                     Cafetería de la UTPL                                                      

Catedral de Loja- puertas en parábola  

                                             

Puente en parábola

HIPÉRBOLA

La hipérbola es una sección cónica, una curva abierta de dos ramas que se podrá obtener al cortar un cono recto por un plano oblicuo al eje que impone simetría; y con un ángulo más pequeño que el de la generatriz respecto del eje de revolución.

                                 Formula general de la hipérbola:

                                   x2/a2 - y2/b2 =1    centro (0,0)

Aplicaciones de la Hipérbola en la Arquitectura:

La hipérbola se la utiliza en diseños de edificios, algunos puentes, cubiertas, etc.

Planta de la Iglesia del Escolasticado de San Pedro Mártir

Padres Dominicos en Alcobendas.

1955. Madrid.

Fuentes bibliográficas:
http://www.monografias.com/trabajos82/conicas-y-aplicaciones/conicas-y-aplicaciones.shtml
http://www.ditutor.com/geometria_analitica/secciones_conicas.html
http://www.vadenumeros.es/primero/conicas-circunferencia-y-elipse.htm
http://www.vitutor.com/geo/coni/fActividades.html
http://mateunfv.blogspot.com/
http://www.construccion-y-reformas.vilssa.com/articulos/el-circulo-en-arquitectura
http://www.mat.ucm.es/~jesusr/expogp/pdfs/expogp/geop14.pdf
http://es.slideshare.net/LuisSoto32/diagramacion-en-arquitectura
https://es.scribd.com/doc/104704046/diagramacion-en-arquitectura
http://laelipse.awardspace.com/

MATRICES

Primero definamos que es una matriz, pues bien es la forma de organizar cierto tipo de datos, que estén dentro del mismo campo, y así poder relacionarlas. Donde a las mismas se las colca dentro de estas tres, parámetros; una columna, casillas horizontales y casillas diagonales, tomando en cuenta los siguientes criterios:

- Relación necesaria: es la relación indispensable entre dos o más espacios.         Ejemplo: comedor y cocina, el espacio que sirve es la cocina y el servido es el     comedor; si no existe la cocina, quien sirve al comedor?

- Relación Deseable: En este tipo de relación la dependencia no es total y la         proximidad de los espacios es solamente “deseable”, ejemplos: sala y garaje,     comedor y despensa

- Relación Inexistente: Cuando no existe ningún tipo de relación entre los             espacios, ejemplo: sala visitas y dormitorio de servicio

Matriz de relaciones ponderadas

En esta parte se divide la matriz (generalmente: social, semisocial, servicio y privada) y coloreando cada una de las áreas así: 

   - Área Social en color verde 

   - Área semisocial en color naranja

   - Área Servicio en color amarillo

   - Área Privada en color rojo

Donde los colores representan, el tipo de circulación, por ejemplo, el rojo, es restricción, el verde libre circulación, etc.

Se interrelacionan los espacios (ambientes) cruzándolos en la franjas diagonales, colocando en el espacio de intersección el numero asignado de acuerdo al tipo de relación que estos tengan entre sí. Este proceso hay que realizarlo con todos los espacios

(uno por uno), partiendo de arriba hacia abajo.

Seguidamente deben sumarse los valores contenidos dentro de las dos columnas diagonales (hacia arriba y hacia abajo) quele corresponden a cada ambiente (exceptuando el primero y el ultimo de la lista, a los que les corresponde únicamente una columna diagonal, ver figura No.1), la suma debe hacerse en forma diagonal (hacia arriba y hacia abajo) y el total de esta se coloca en las casillas que dicen sumatoria, ver matrices a continuación.

Finalmente se establecen rangos de acuerdo a las sumatorias obtenidas, estos se establecen de forma descendente de acuerdo a la sumatoria, esto quiere decir, que el rango 1 será el de la cantidad mayor obtenida en la sumatoria y el último rango será la sumatoria de menor. Al final debe realizarse un resumen de la ubicación de los ambientes de acuerdo al rango, este a la par de la matriz.

Fuentes Biliograficas: 

http://www.monografias.com/trabajos82/conicas-y-aplicaciones/conicas-y-aplicaciones.shtml

http://www.ditutor.com/geometria_analitica/secciones_conicas.html

http://www.vadenumeros.es/primero/conicas-circunferencia-y-elipse.htm

http://www.vitutor.com/geo/coni/fActividades.html

http://mateunfv.blogspot.com/

http://www.construccion-y-reformas.vilssa.com/articulos/el-circulo-en-arquitectura

http://www.mat.ucm.es/~jesusr/expogp/pdfs/expogp/geop14.pdf

http://es.slideshare.net/LuisSoto32/diagramacion-en-arquitectura

https://es.scribd.com/doc/104704046/diagramacion-en-arquitectura

FUNCIONES

Una función es una relación o correspondencia entre dos magnitudes, de manera que a cada valor de la primera le corresponde un único valor de la segunda (o ninguno), que llamamos imagen o transformado.

A la función se le suele designar por f y a la imagen por f(x), siendo x la variable independiente.

   - Variable independiente: la que se fija previamente

  - Variable dependiente: La que se deduce de la variable independiente.

Las funciones son como máquinas a las que se les introduce un elemento x y devuelven otro valor y, que también se designa por f(x).

Por ejemplo, la función f(x) = 3x2 + 1 es la que a cada número le asigna el cuadrado del número multiplicado por 3 y luego sumado 1.

Así f(2) = 3*22 + 1= 3*4 + 1 = 12 + 1 = 13

FUNCION EXPONENCIAL

Definición: Una función exponencial con base b es una función de la forma f(x)=bx , donde b  y  x son números reales tal que b > 0  y  b es diferente de uno.

El dominio  es el conjunto de todos los números reales y el recorrido es el conjunto de todos los números reales positivos.

La función exponencial puede considerarse como la inversa de la función logarítmica, por cuanto se cumple que:

              Representación gráfica de varias funciones exponenciales

Función exponencial, según el valor de la base.

Propiedades de las funciones exponenciales

Para toda función exponencial de la forma f(x) = ax, se cumplen las siguientes propiedades generales:

La función aplicada al valor cero es siempre igual a 1:

            f (0) = a0 = 1.

La función exponencial de 1 es siempre igual a la base:

f (1) = a1 = a.

La función exponencial de una suma de valores es igual al producto de la aplicación de dicha función aplicada a cada valor por separado.

f (x + x?) = ax+x? = ax × ax? = f (x) × f (x?).

La función exponencial de una resta es igual al cociente de su aplicación al minuendo dividida por la función del sustraendo:

f (x - x?) = ax-x? = ax/ax? = f (x)/f (x?).

La función ex

Un caso particularmente interesante de función exponencial es f (x) = ex. El número e, de valor 2,7182818285..., se define matemáticamente como el límite al que tiende la expresión:

(1 + 1/n)n

APLICACIÓN DE LA FUNCIÓN EXPONENCIAL EN LA ARQUITECTURA:

Un ejemplo de cómo utilizar esta función en la arquitectura se da en lo siguiente:

El matemático Weidman dedujo la base para la construcción de la torre. Un factor crucial para los cálculos que Eiffel tenía en mente pasaba por calibrar el efecto de las fuerzas ejercidas por el viento sobre determinados puntos estructurales de la Torre. Weidman encontró una solución exacta de la ecuación en forma de una función exponencial que se ajusta rigurosamente a la forma de la mitad superior de la torre.

La clave para su solución deriva dedos ecuaciones exponenciales diferentes interconectadas: una para la mitad superior de la torre, y otra en la que interviene el factor de sobredimensionamiento de seguridad de la estructura en su base.

FUNCIÓN LOGARÍTMICA

Una función logarítmica es aquella que genéricamente se expresa como f(x) =logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.

La función logarítmica es la inversa de la función exponencial , dado que:

loga x = b Û ab = x.

                           Representación gráfica de funciones logarítmicas y de sus inversas                                                       (exponenciales).

Propiedades de la función logarítmica

Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la función exponencial. Así, se tiene que:

La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (0,+¥).

Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales, luego el recorrido de esta función es R.

En el punto x = 1, la función logarítmica se anula, ya que loga 1 = 0, en cualquier base.

La función logarítmica de la base es siempre igual a 1.

Finalmente, la función logarítmica es continua, y es creciente para a > 1 y decreciente para a < 1.

FUNCIÓN TRIGONOMÉTRICA

Una función trigonométrica, también llamada circular, es aquella que se define por la aplicación de una razón trigonométrica a los distintos valores de la variable independiente, que ha de estar expresada en radianes. Existen seis clases de funciones trigonométricas: seno y su inversa, la cosecante; coseno y su inversa, la secante; y tangente y su inversa, la cotangente. Para cada una de ellas pueden también definirse funciones circulares inversas: arco seno, arco coseno, etcétera.

La función seno:

La función seno es periódica, acotada y continua, y su dominio de definición es el conjunto de todos los números reales.

La función cosecante puede calcularse como la inversa de la función seno expresada en radianes.

Gráfica de la función seno.

La función coseno:

La función coseno, que se denota por f (x) = cos x. Esta función es periódica, acotada y continua, y existe para todo el conjunto de los números reales.

La función secante se determina como la inversa de la función coseno para un ángulo dado expresado en radianes.

Gráfica de la función coseno.

La función tangente:

Esta función se expresa genéricamente como f (x) = tg x, siendo x la variable independiente expresada en radianes.

La función cotangente es la inversa de la tangente, para cualquier ángulo indicado en radianes.

APLICACIÓN DE LA FUNCIÓN TRIGONOMÉTRICA EN LA ARQUITECTURA

La matemática hace el diseño de edificios más seguro y más preciso. La trigonometría es especialmente importante en la arquitectura, ya que permite al arquitecto calcular las distancias y las fuerzas relacionadas con elementos de la diagonal. De las seis funciones de trigonometría básicas, el seno, el coseno y la tangente son los más importantes para la arquitectura, ya que permiten al arquitecto encontrar fácilmente los valores opuestos y adyacentes relacionados con un ángulo o la hipotenusa, la traducción de un vector diagonal en vectores horizontales y verticales.

Para el diseño de planos, cálculo de resistencia de materiales, tratamos con modelos geométricos, en los cuales las funciones trigonométricas son de gran ayuda.

EJEMPLO

Resolveremos el siguiente problema propuesto, hallado lo valores que faltan.Donde a=300 y b=380. Hallar los angulos y la hipotenusa.

Hipotenusa                           Angulo α                              Angulo β

C²= a² + b²                     Sen α= cta. ops/hipt.               β=180^o - (α + 90^o)

C²=(300m)²+(380m)²        Sen α= a/c                            β=180^o-(52^o + 90^o)

C= 484m                         Sen α= 300/484                       β= 38^o
                                      Sen α= 52^o

FUNCION ALGEBRAICA

En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.

Las funciones algebraicas pueden ser:

Funciones explícitas:

En las funciones explícitas se pueden obtener las imágenes de x por simple sustitución.

f(x) = 5x – 2

Funciones implícitas:

En las funciones implícitas no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.

5x - y - 2 = 0

Funciones polinómicas:

Las funciones polinómicas vienen definidas por un polinomio.

f(x) = a0 + a1 x + a1 x² + a1 x³ +··· + an xn

Su dominio es  , es decir, cualquier número real tiene imagen.

Funciones Constantes:

El criterio viene dado por un número real.

f(x)= k

La gráfica es una recta horizontal paralela a al eje de abscisas.

Funciones polinómica de primer grado:

f(x) = mx +n

Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.

Funciones cuadráticas:

f(x) = ax² + bx +c

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

Funciones racionales:

El criterio viene dado por un cociente entre polinomio:

EJEMPLO DE FUNCIÓN CUADRÁTICA.

El puente Golden Gate enmarca la entrada a la bahía de San Francisco. Sus torres de 746 pies de altura están separadas por una distancia de 4200 pies. El puente está suspendido de dos enormes cables que miden 3 pies de diámetro: el ancho de la calzada es de 90 pies y ésta se encuentra aproximadamente a 220 pies del nivel del agua. Los cables forman una parábola y tocan la calzada en el centro del puente. Determinar la altura de los cables a una distancia de 1000 pies del centro del puente.

Solución.

Empezarnos seleccionando la ubicación de los ejes de coordenadas de modo que el eje x coincida en la calzada y el origen coincida en el centro del puente.
Como resultado de esto, las torres gemelas quedarán a 746-220=526 pies arriba de la calzada y ubicadas a 42002=2100 pies del centro.
Los cables de forma parabólica se extenderán desde las torres, abriendo hacia arriba, y tendrán su vértice en (0,0) como se ilustra en la figura de abajo

La manera en que seleccionamos la colocación de los ejes nos permite identificar la ecuación de una parábola como

y=ax2,a>0.

Obsérvese que los puntos (−2100,526) y (2100,526) están en la gráfica parabólica.

Anexos: 

Fuentes bibliográficas:

http://recursostic.educacion.es/descartes/web/materiales_didacticos/funciones_estudio_golbal_eda05/concepto_funcion.htm

http://www.vitutor.com/fun/2/c_1.html

http://www.hiru.com/matematicas/funcion-exponencial

http://xombit.com/2011/06/la-importancia-de-las-matematicas-en-el-diseno-i

http://www.hiru.com/matematicas/funcion-logaritmica

http://www.ditutor.com/funciones/funcion_algebraica.html

http://www.ehowenespanol.com/trigonometria-arquitectura-como_127481/

LIMITES

Es la aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.

LIMTE DE UNA FUNCIÓN

Una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.

Ejemplo 1:

Ejemplo 2:
En la tabla se muestra la aproximación del valor "x" (sombreado de verde) al número 2, en la columna adyacente esta como el de "y" se aproxima a 3.

LIMITES UNILATERALES

Para analizar el límite de una función en un punto, es necesario acercarse a ese punto tanto por derecha como por izquierda, a esta forma de acercarse al punto analizado por los lados se le conoce como Límites Laterales y se simboliza por:

De hecho, para poder decir que el límite en un punto existe, se debe verificar que el límite de f(x) por la izquierda es igual al límite de f(x) por la derecha, por ejemplo:

En el caso A, se ve que cuando Xo se acerca a 2 por la izquierda (X0-), la imagen de f(x) se acerca a 4 por abajo, mientras que si Xo se acerca por la derecha(X0+), la imagen se acerca a 4 por arriba. En ambos casos la imagen se acerca a 4, por lo tanto, el límite de f(x) cuando Xo se acerca a 2, es 4.

En el caso B, Xo se acerca a 2 y su imagen se acerca a 2, pero cuando Xo se acerca por la derecha, se ve que la imagen se acerca a 0. En este caso las imágenes se acercan a diferentes valores por lo tanto se dice que no hay un límite cuando Xo se acerca a 2.

Ejemplo 1:

                                                          

Ejemplo 2:

       

 LIMTES INFINITOS

             

si x = 0+ los valores de la función crecen indefinidamente.

si x = 0- los valores de la función decrecen indefinidamente.

Las dos ramas de la curva se acercan cada vez más al eje y a medida que x se aproxima a cero.

Para esta gráfica la recta x = 0 es asíntota vertical.

                                                               

si x = 1+ los valores de la función decrecen indefinidamente. si x = 1- 

los valores de la función crecen 

indefinidamente.

Las dos ramas de la curva se acercan 

cada vez más a la recta  x = 1 a medida 

que x se aproxima a ese valor.

Para esta gráfica la recta 

x = 1 es asíntota vertical.

        

         

si x = 0+ los valores de la función crecen

 indefinidamente.

si x = 0- los valores de la función 

crecen indefinidamente.

Para esta gráfica la recta x = 0 es asíntota vertical.

                                                                  

                   

si x = 0+ los valores de la función 

decrecen indefinidamente.

si x = 0- los valores de la función 

decrecen indefinidamente

Nota. Cuando se refiere a límites infinitos en realidad no son límites sino que proporcionan símbolos y un lenguaje útiles para describir el comportamiento de funciones cuyos valores se hacen arbitrariamente grandes (positivos o negativos).

Ejemplo: lim  5-x/x-2

(n→5)

Limite por la izquierda                            Límite por la izquierda

lim  5-1,999/1,999-2                                  lim  5-2,001/2,001-2  

(n→5)                                                       (n→5)             

lim  3,001/- 0,001 = -∞                             lim   2,999/0,001= +∞

(n→5)                                                       (n→5)      
     

CONTINUIDAD EN UN PUNTO

Una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua Una función continua de   en   es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel (más formalmente su grafo es un conjunto conexo).

Una función es continua en un punto x = a si existe límite de la función en él y coincide con el valor que toma la función en dicho punto, es decir: 

Limx → a+f(x) = limx → a−f(x) = f(a)

La continuidad de una función f en el punto x = a implica que se cumplan las tres condiciones siguientes: 

1. Existe el límite de la función f(x) en x = a.
2. La función está definida en x = a; es decir, existe f(a)
3. Los dos valores anteriores coinciden.

Grafica de una función continua:

CONTINUIDAD EN UN INTERVALO

Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:
1. Que el punto x = a tenga imagen.
                                             
2. Que exista el límite de la función en el punto x = a.
                                 
3. Que la imagen del punto coincida con el límite de la función en el punto.
                                           

Continuidad de una función en un intervalo abierto

Una función es continua en un intervalo abierto o unión de intervalos abiertos si es continua en cada punto de ese conjunto.
Decimos que f(x) es continua en (a, b) sí y sólo sí f(x) es continua " x Î (a, b).

EJEMPLO:                                                                     

Analice la continuidad de la función 

 h(x) =en el intervalo (–1, 1).

Por ser una función racional, la función es continua en cada número real excepto los que anulan el denominador, x = 1 y x = -1. Como esos valores no pertenecen al intervalo, la función es continua en el intervalo (–1,1).

Continuidad de una función en un intervalo cerrado

La continuidad de una función en un intervalo cerrado [a, b] no es sencilla de analizar como en el caso de intervalos abiertos. Dado que al considerar el intervalo cerrado [a, b] la función no está definida a la izquierda de a como tampoco a la derecha de b, no tiene sentido considerar los límites en a y en b. Esto hace que no se pueda definir la continuidad en esos dos puntos. Se debe definir primero la continuidad por derecha y la continuidad por izquierda en un punto.

APLICACION DE LIMITES EN LA ARQUITECTURA
El arquitecto como profesional debe garantizar seguridad y un buen diseño en sus construcciones para eso el estudio de los limites es muy importante, ya que mediante la aplicación de límites podemos calcular cual es el soporte de un terreno para la construcción de una edificación y cuál sería su límites de plantas que se pudieran construir soportar el terreno.

Para comenzar una edificación hay que saber las condiciones de nuestro terreno para así saber cuál son nuestros límites de plantas que se puede alzar en ese espacio según su estado de soporte estructural en el terreno que sobre todo nos brinde seguridad y para  también poder saber cuál son nuestros límites de espacio que se puede construir según las medidas del terreno.

También se aplican los límites para saber cuál son las distancias  que se tiene que guardar entre construcciones dependiendo los terrenos.

Fuentes Bibliográficas:

http://es.wikipedia.org/wiki/L%C3%ADmite_de_una_funci%C3%B3n

http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/limitesycontinuidad/html/node7.html

http://www.fca.unl.edu.ar/Limite/2.3%20L%EDmites%20Infinitos.htm

http://es.wikipedia.org/wiki/Funci%C3%B3n_continua

http://www.buenastareas.com/ensayos/Definicion-De-Continuidad-En-En-Un/2038289.html

http://www.iesayala.com/selectividadmatematicas/ficheros/teoria/analisis/06_FUNCIONES_CONTINUAS.pdf

http://www.fca.unl.edu.ar/Continuidad/3.2%20Funci%F3n%20continua%20en%20unintervalo.htm

DERIVADAS 

El concepto de derivada de una función matemática se halla íntimamente relacionado con la noción de límite. La derivada se entiende como la variación que experimenta la función de forma instantánea, es decir, entre cada dos puntos de su dominio suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales.

La derivada de una función es un concepto local, es decir, se calcula como el limite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

REGLAS DE DERIVACIÓN Las reglas de derivación son los métodos que se emplean para el cálculo de la derivada de una función. Dependiendo del tipo de función se utiliza un método u otro.

1. LA DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN es igual a la constante por la derivada de la función:

2.LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a la suma de las derivadas de las funciones:

3. LA DERIVADA DE UNA DIFERENCIA DE FUNCIONES es igual a la diferencia de las derivadas de las funciones:

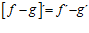4. LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función sin derivar más la primera función sin derivar por la derivada de la segunda función:

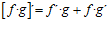5. LA DERIVADA DE UN COCIENTE DE FUNCIONES es igual a la derivada de la función del numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la derivada de la función del denominador, dividido todo ello por la función del denominador al cuadrado:

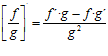6. LA DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA es igual a la derivada de la expresión como exponencial más la derivada de la expresión como potencial:

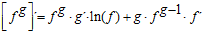Regla de la cadena:

la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones.

Descripción de la regla En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser computado como el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.

Ejemplo:

Tomando f(x) = x³, obtenemos

d dx

u3

=

3u2

du dx

En palabras:

La derivada de una cantidad al cubo es igual a 3 veces la cantidad (original) al cuadrado por la derivada de la cantidad.

Ejemplo 2:

d dx

(1+x2)3

=

3(1+x2)2 d dx (1+x2)

=	3(1+x2)2,2x

=

6x(1+x2)2

CRITERIO DE LA PRIMERA DERIVADA

Se llama Criterio de la primera derivada al método o teorema utilizado frecuentemente en el calculo matemático para determinar los mínimos y máximos relativos que pueden existir en una función mediante el uso de la primera derivada o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto critico 

EJEMPLO:
A partir de la siguiente función encuentre:
a)Los puntos críticos.
b)Valores máximos y mínimos.
c)La gráfica de la función.

f(x)= 4x2 + 5x - 3

a) PUNTOS CRÍTICOS:
- obtener la derivada de la función:
8x + 5
- igualar con cero (0).
f'(x)= 8x + 5 = 0
x = -5/8

b)MÁXIMOS Y MÍNIMOS:

- El punto crítico lo podemos obtener igualando con cero (0) la función derivada y despejando "x".

- El valor de antes y después lo podemos obtener con un número menor (antes) que el punto crítico y un número mayor (después) que el punto crítico.

- La primera derivada la podemos obtener sustituyendo el valor de antes y después en la primera derivada. 

- El comportamiento lo podemos deducir de la siguiente manera: Si el número de la primera derivada es positivo "sube", si el número es negativo "baja". 

- El resultado lo deducimos de la siguiente manera: Si primero "baja y luego sube" su resultado es Mínimo. Si el comportamiento es "Sube y luego baja" el resultado Máximo.

c)GRÁFICA:
La gráfica la podemos obtener sustituyendo en la función original el punto crítico y asi obteniendo los puntos del mínimo absoluto de la gráfica.

CRITERIO DE LA SEGUNDA DERIVADA

El Criterio o prueba de la segunda derivada es un teorema o método del calculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.

Se basa en el hecho de que si la gráfica de una función  es convexa en un intervalo abierto que contiene a , y  debe ser un mínimo relativo de. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y  debe ser un máximo relativo de .

Valores máximos y mínimos:

Criterio de la segunda derivada para estabecer los valores maximos y minimos de una función. Ademas de proporcionar información sobre la concavidad de la gráfica de una función, la segunda derivada permite establecer si un punto critico es un valor máximo o un valor mínimo.

Ejemplo:

,

Note que la función f no está definida en 

La derivada de f está dada por , 
Los valores críticos de f se obtienen cuando . En este caso,  si y solo si , ó .
Ahora, la segunda derivada de f es 
Vamos a evaluar  en  y en 

a.	; como  entonces  es un valor mínimo relativo de f.
b.	; como  entonces  es un valor máximo relativo de f.

Gráficamente se tiene en el intervalo  

EJEMPLO:
El criterio de la segunda derivada proporciona la concavidad de una curva de la siguiente manera.

a) Puntos críticos.
b) Valores máximos y mínimos.
c) Punto de inflexión.
d) La gráfica de la función.

f(x) = 3x^2 + 5x - 2

a) Puntos críticos:
f'(x)6x + 5 = 0
x = -5/6
x = -0.83

- Para obtener el punto crítico se debe de despejar la "x" en la primera derivada.

- Para obtener la segunda derivada se debe de sacar la segunda derivada y despejar la "x" si es el caso.

- La concavidad se puede deducir dependiendo del resultado de la segunda derivada. Si es positivo la concavidad estará feliz. Si es negativo la concavidad estará triste.

- El resultado también depende de la segunda derivada, si aumenta dependiendo del punto crítico, es mínimo, si disminuye dependiendo del punto crítico entonces será máximo.

c) PUNTO DE INFLEXIÓN:
- Igualar la segunda derivada con cero (0). (en este caso no hay punto de inflexión)

d) GRÁFICA:
- Sustituyes en la función original el punto crítico.(hay casos en que son dos puntos críticos)
- Sustituyes en la función original el punto de inflexión.
- Gráficas.
                                             

APLICACIÓN DE LAS DERIVADAS EN LA ARQUITECTURA

las derivadas se utilizan para poder conocer las superficies parabolicas o superficies orgánicas irregulares de una construccion, con un minucioso estudio, ya que muchas veces no se puede determinar esto con operaciones comunes sino que hay que recurrir a las derivadas para poder ser exactos, al encontrar los puntos máximos y mínimos, punto de infelxion,etc  

rascacielos Torre Metro de Shenzhen

Porsche Pavilion por HENN, instalaciones en Alemani

Tambien se las utliza en la construcción de las maquinas de parques de juegos, ya que su funcionalidad es compleja, ya que muchos de los juegos tienden a tener un movimiento hacia arriba y hacia abajo por lo que se necesita del calculo exacto hasta donde y puede subir y cuando tiene que descender.

    




parques de atracciones de SimCity




fuentes bibliograficas:

http://www.derivadas.es/

http://www.vitutor.com/fun/4/b_a.html
http://es.wikipedia.org/wiki/Derivada
http://profecarlinis.galeon.com/aficiones1608405.html
https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesderivada/html/node6.html
http://profecarlinis.galeon.com/album1608406.html

INTEGRALES

Proceso que permite restituir una función que ha sido previamente derivada. Es decir, la operación opuesta de la derivada asi como la suma es a la resta.

Por conveniencia se introduce  una notación para la antiderivada de una función

Si F^!(x) = f(x),  se representa 

A este grafo ∫ se le llama símbolo de  la integral y a la notación∫f x  dx se le llama integral indefinida  de f(x) con respecto a x. La función f(x)se denomina integrando, el proceso recibe el nombre de integración. Al número C se le llama    conste de integración esta surge por la imposibilidad  de la constante derivada. Así como dx denota diferenciación son respecto a la variable x, lo cual indica la variable derivada.

∫f x  dx

Esto se lee integral de fx del diferencial de x

Propiedades

·          ∫  kfx  dx = k ∫f x  dx

·         ∫ (f x+ gx)  dx = ∫f x  dx + ∫g x  dx

Formulas de Integracion

Estas son las formulas de integración, podrán integrar funciones logarítmicas  trigonométricas  exponenciales, hiperbólicas y sus respectivas derivadas; estas formulas les facilitaran mas el calculo integral, también están varias identidades trigonométricas.

Integrales mas comunes

∫ k dx = kx + c     ------------------------------> la letra k es una constante 

∫ k f(x) = k ∫ f(x) + c

∫ uⁿ du = uⁿ⁺¹ / n+1

∫ u^n-1 du = ln|u|+c

Integrales trigonométricas 

∫ sen u du = -cos u + c 

∫ cos u du = sen u + c

∫ sec u tan u du = sec u + c

∫  sec² u du = tan u + c

∫ csc u cot u du = -csc u + c

∫ csc² u du = -cot u + c

Integrales trigonométricas inversas

Integrales exponenciales 

∫ e^u du = e^u + c 

Integrales logarítmicas y trigonométricas 

∫ tan u du = -ln | cos u | + c

∫ cot u du = ln | sen u | + c

∫ sec u du = ln | sec u + tan u | + c 

∫ csc u du = -ln |csc u + cot u | + c

Integrales Hiperbólicas

∫ cosh u du = senh u + c

∫ senh u du = cosh u + c

∫ sech² u du = tanh u + c

∫ cosh² u du = -csch u + c

∫ sech u tanh u du = -sech + c

∫ csch u coth u du = -csch u + c 

Integrales por sustitución 
El método de integración por sustitución o cambio de variable se basa en la regla de la cadena.

El método se basa en identificar una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga unaintegral más sencilla.

Pasos para integrar por sustitución

1º Se hace el cambio de variable y se diferencia en los dos términos:

Se despeja u y dx, sutituyendo en la integral:

2º Si la integral resultante es más sencilla, procedemos a integrar:

3º Se vuelve a la variable inical:

Ejemplo 1:

Ejemplo 2:

             

Intergrales por partes

El método de integración por partes se basa en la derivada de un producto y se utiliza para resolver algunasintegrales de productos.




Tenemos que derivar u e integrar v', por lo que será conveniente que la integral de v' sea inmediata.
Las funciones polinómicas, logarítmicas y arcotangente se eligen como u.
Las funciones exponenciales y trígonométricas del tipo seno y coseno, se eligen como v'.

Ejemplo 1:

 

Ejemplo 2:

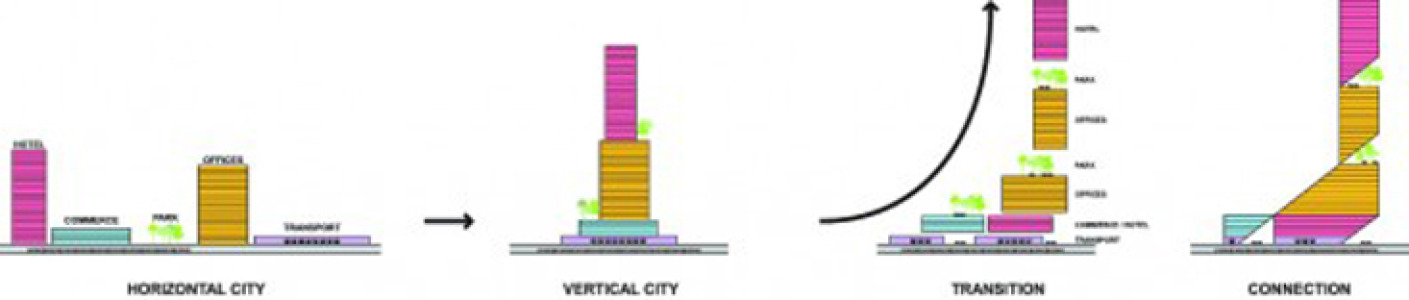
APLICACIÓN DE LAS INTEGRALES EN LA ARQUITECTURA

el uso de las integrales tiene un fin especifico, el generar y crear en la arquitectura proyectos con formas  complejas y dinámicas.

Los procesos geométricos y de calculo nos permiten manipular con mayor precisión nuestro diseño para llegar a resultado óptimos.

Su aplicación se centra en edificios que tienen una figura amorfa , donde el calculo de su área resulta un poco complejo es por ello que se implementan las integrales definidas.

   

Recuerda que las integrales definidas representan el área limitada por la grafica de una función ( curvas y rectas ) 

    

En el campo de las construcciones, los arquitectos, ingenieros y profesionales de estas áreas usualmente emplean la integral para obtener el área de superficies irregulares. 

Fuentes bibliograficas:

http://www.calculointegrales.com/p/concepto-de-integral.html
http://mateaprendizaje.blogspot.com/2013/03/formulas-de-integracion.html
http://www.inetor.com/metodos/integracion_partes.html
http://es.wikipedia.org/wiki/M%C3%A9todos_de_integraci%C3%B3n#M.C3.A9todo_de_integraci.C3.B3n_por_partes
http://es.slideshare.net/franklingualaquiza/aplicacin-de-la-integral-definida-en-la-arquitectura